Random Forests Quantile Classifier (RFQ)
Hemant Ishwaran
Robert O’Brien
Min Lu
Udaya B. Kogalur
2023-05-29
imbalance.Rmd
Introduction
Imbalanced data, or the class imbalance problem, refers to classification settings involving two classes where the ratio of the majority class to the minority class is much larger than one. This latter quantity is known as the imbalance ratio \(\left(\mathrm{IR}\right)\).
As an example, a causal analysis was used to analyze observational data from a study of adjuvant therapy versus surgery in esophageal cancer patients. As part of this analysis a random forests (RF) classifier was used to to assess treatment overlap. However this turned out to be problematic due the fact that the data was imbalanced. In this study, there were 6649 surgery patients and 988 adjuvant therapy patients, an imbalanced ratio of \(6649/988=6.73\).
Running RF classification yielded the confusion matrix given below. The overall misclassification error is fairly low, 12.2%, which suggests the classifier is doing a good job, however this turns out to be deceiving upon more careful inspection of the matrix. Conditioning on the two class labels we obtain performance rates of .988 for surgery (true negative rate, TNR) and .140 for adjuvant therapy (true positive rate, TPR). While .988 is very high, we can see this is artificially inflated due to the fact that the classifier is over-classifying cases to the majority class, surgery. This leads to the poor performance of .140 for adjuvant therapy since many of these cases are falsely classified.
| \(\quad\) | \(\quad\) | predicted | \(\quad\) | \(\quad\) |
|---|---|---|---|---|
| \(\quad\) | surgery | adjuvant | error | \(\quad\) |
| surgery | 6567 | 82 | .012 | .988 = TNR |
| adjuvant | 850 | 138 | .860 | .140 = TPR |
Overall error rate: 12.2%
Bayes decision rule
Why does this happen? Class imbalanced data seriously hinders the classification performance of learning algorithms such as RF because their decisions are based on the Bayes rule. The Bayes rule is the de facto method used in machine learning. It is used because it is the decision rule that minimizes misclassification error, which at first seems like a good property. But this is problematic for imbalanced data since misclassification error is often minimized by classifying most (if not) all of the data as belonging to the majority class. More formally, let \(Y\in\{0,1\}\) denote the two-class outcome and let \(p({\bf x}) = \mathbb{P}\{Y = 1 \mid {\bf X}= {\bf x}\}\) be the classification probability for the minority group. The Bayes rule classifies cases to class label 1 if the classification probability is \(1/2\) or larger, \[ \delta_{\textrm B}({\bf x})=I{\{p({\bf x}) \ge 1/2\}}. \] The problem is that \(p({\bf x})\) is small in imbalanced problems. This forces the Bayes decision rule to classify all cases to class label 0 as the \(\mathrm{IR}\) increases. Indeed, in the limit: \[ \delta_{\textrm B}({\bf x})=I{\{p({\bf x}) \ge 1/2\}}\rightarrow 0, \quad\text{if } p({\bf x}) \rightarrow 0. \] This seemingly works out for the Bayes decision rule, because [as will be shown in equation (1)] this yields a misclassification error rate of zero. But is this really a good thing?
Formal definitions of imbalanced
Our goal is to build an accurate classifier for \(Y\) given \({\bf X}={\bf x}\) when the learning data is imbalanced. To help quantify what is meant by imbalancedness, we provide the following formal definitions, beginning with the imbalance ratio described earlier. Following the convention in the literature, we assume that the majority class labels are 0, and outnumber the minority class labels, 1.
Definition 1: The imbalance ratio \(\left(\mathrm{IR}\right)\) is defined as \(\mathrm{IR}=N_0/N_1\) where \(N_0\) and \(N_1\) denote the cardinality of the majority and minority samples, respectively. A data set is imbalanced if \(\mathrm{IR}> 1\).
For example, the \(\mathrm{IR}\) in our previous example was 6.73. This is actually only moderately high and in practice it is possible to encounter data with much higher values. In fact, we will examine a simulation setting where the value is allowed to be 100.
Definition 2: A minority class example is safe, borderline, or rare if 0 to 1, 2 to 3, or 4 to 5 of its 5 nearest neighbors are of the majority class, respectively.
The percentage of minority class samples that are rare plays an important role in the performance of a classifier.
Definition 3: The data is marginally imbalanced if \(p({\bf x})\ll 1/2\) for all \({\bf x}\in\mathscr{X}\) where \(p({\bf x})=\mathbb{P}\{Y=1|{\bf X}={\bf x}\}\).
Thus, marginally imbalanced data is data for which the probability of the minority class is close to zero throughout the feature space.
Definition 4: The data is conditionally imbalanced if there exists a set \(A\subset\mathscr{X}\) with nonzero probability, \(\mathbb{P}\{{\bf X}\in A\}>0\), such that \(\mathbb{P}\{Y=1|{\bf X}\in A\}\approx 1\) and \(p({\bf x})\ll 1/2\) for \({\bf x}\notin A\).
In contrast to marginally imbalanced data, conditional imbalancedness occurs when the probability of the minority class is close to 1 given the features lie in a certain set, and approximately zero otherwise. In both cases, it is assumed that the minority class is rare.
Quantile classifiers
Following [1], we define a quantile classifier (\(q\)-classifier) as \[ \delta_{\textrm q}({\bf x}) = I{\{p({\bf x}) \ge q\}},\quad\text{} 0<q<1. \] Observe that the median classifier \(q\) = 1/2 yields the Bayes classifier \[ \delta_{\textrm B}({\bf x})=I{\{p({\bf x}) \ge 1/2\}}. \] Define the cost-weighted risk for a classifier \(\delta:\mathscr{X}\rightarrow\{0,1\}\) as \[ r(\delta,\ell_0,\ell_1) = \mathbb{E}\left[ \ell_0 I{\{\delta({\bf X})=1, Y=0\}} + \ell_1 I{\{\delta({\bf X})=0, Y=1\}} \right] \] where \[\begin{eqnarray} \ell_0 > 0 && \text{cost of misclassifying a majority case}\\ \ell_1 > 0 && \text{cost of misclassifying a minority case}. \end{eqnarray}\] We have the following result which states that under cost-weighted risk the optimal classifier is the weighted Bayes rule.
Theorem 1: Under cost-weighted risk, the optimal classifier is the weighted Bayes rule \[ \delta_{\textrm{WB}}({\bf x})=I{\{p({\bf x}) \ge \ell_0/(\ell_0+\ell_1)\}} \] which we recognize as a quantile classifier with \(q = \ell_0/(\ell_0+\ell_1)\) and its risk is \[ r(\delta_{\textrm{WB}}, \ell_0,\ell_1) = \mathbb{E}\left[\min \{\ell_1 p({\bf X}), \ell_0(1-p({\bf X}))\}\right]. \]
The Bayes rule is the median quantile rule corresponding to \(q=1/2\) with equal misclassification costs \(\ell_0=\ell_1=1\). Thus, its cost-weighted risk is
Optimality goal
We see that classification error provides a strong incentive for learning algorithms to correctly classify majority class samples at the expense of misclassifying minority class samples. This is obviously problematic.
So what is a way out of this dilemma? One solution is to notice that the Bayes rule uses equal misclassification costs and therefore uses the \(q\)-threshold of 0.5. Thus a way out is to select another value of \(q\). But what is a reasonable way to do this?
It turns out that we can solve this problem by attacking it from a different angle. Our previous example involving cancer patients serves to illustrate that in the presence of class imbalance data, learning algorithms should be evaluated based on the samples classified correctly within each class, known as the true positive rate (TPR) for the minority class and the true negative rate (TNR) for the majority class, instead of misclassification error (ERR), which makes no such distinction. Formally, these values are defined as follows: \[ \textrm{TPR}=\frac{\textrm{TP}}{\textrm{TP}+\textrm{FN}},\hskip10pt \textrm{TNR}=\frac{\textrm{TN}}{\textrm{TN}+\textrm{FP}},\hskip10pt \textrm{ERR} = \frac{\textrm{FP}+ \textrm{FN}}{\textrm{TP}+ \textrm{FN}+ \textrm{TN}+ \textrm{FP}}. \]
| \(\quad\) | Predicted | Class |
|---|---|---|
| Observed Class |
\(\quad\) 0 |
\(\quad\) 1 |
| 0 | TN | FP |
| 1 | FN | TP |
Table1: Confusion Matrix. TN = True Negative, FP = False Positive, FN = False Negative, and TP = True Positive
Our goal is to find a classifier that achieves both high TNR and TPR values in imbalance problems. We call this property TNR+TPR optimal.
Definition 5: A classifier \(\delta:\mathscr{X}\rightarrow\{0,1\}\) is said to be TNR+TPR-optimal if it maximizes the sum of the rates, TNR \(+\) TPR.
Define the TNR (true negative) and TPR (true positive) value for a classifier \(\delta\) as follows: \[ \textrm{TNR}(\delta)=\mathbb{P}\{\delta({\bf X})=0|Y=0\},\hskip15pt \textrm{TPR}(\delta)=\mathbb{P}\{\delta({\bf X})=1|Y=1\}. \] Notice that the Bayes rule, \(\delta_{\textrm B}\), is unlikely to achieve this goal because it has a TNR value of 1 but a TPR value of 0 in the limit.
A density-based approach
We introduce the following classifier derived from a density-based approach: \[ \delta_{\textrm D}({\bf x})= I{\left\{\cfrac{f_{{\bf X}|Y}({\bf x}|1)}{f_{{\bf X}|Y}({\bf x}|0)}\,\,\ge\,\, 1\right\}}. \] Basing the classifier on the conditional density of the features, \(f_{{\bf X}|Y}\), rather than the conditional density of the response, \(p({\bf x})\), removes the effect of the prevalence of the minority class.
It can be shown that \(\delta_{\textrm D}({\bf x})\) has the TNR+TPR-property [2]. Therefore we have the optimal classifier we seek. However, while it is convenient theoretically to describe the density-based classifier in terms of the conditional density of the data, in practice it will be difficult to implement the classifier as stated. But using Bayes’ Theorem, we can rewrite \(\delta_{\textrm D}({\bf x})\) more conveniently as \[\begin{eqnarray} \delta_{\textrm D}({\bf x}) &=& I{\left\{\cfrac{f_{{\bf X}|Y}({\bf x}|1)}{f_{{\bf X}|Y}({\bf x}|0)}\,\,\ge\,\, 1\right\}}\\ &=& I{\{\Delta_{\textrm D}({\bf x}) \ge 1\}}, \hskip20pt \Delta_{\textrm D}({\bf x})= \frac{p({\bf x})(1-\pi)}{(1-p({\bf x}))\pi}\\ &=& I{\{p({\bf x})\ge\pi\}}, \hskip27pt\pi=\mathbb{P}\{Y=1\}. \end{eqnarray}\] This shows that the density-based estimator is actually a \(q\)-classifier with the value \(q=\pi=\mathbb{P}\{Y=1\}\). Thus setting \(q\) to the value \(\pi\) which is the prevalence (minority class marginal probability) gives us the optimal value we were after. For example, if the data is balanced, \(\pi=1/2\), then this becomes the Bayes rule. We call this new classifier the q*-classifier [2].
Definition 6: Call \(\delta_{\textrm q^*}({\bf x}) = I{\{p({\bf x})\ge\pi\}}=\delta_{\textrm D}({\bf x})\) the q*-classifier.
The classifier has the following optimality properties.
Theorem 2: The q*-classifier is TNR+TPR-optimal. Furthermore, it is the cost-weighted Bayes rule under misclassification costs \(\ell_0=\pi\) and \(\ell_1=(1-\pi)\) and achieves the optimal weighted risk of zero under both marginal and conditional imbalance.
Notice the q*-classifier achieves the optimal weighted risk \[\begin{eqnarray} r(\delta_{\textrm q^*}, \pi,1-\pi) &=&\mathbb{E}\left[\min \{(1-\pi) p({\bf X}), \pi (1-p({\bf X}))\}\right]\\ &\le& \mathbb{E}\left[\pi(1-p({\bf X}))\right]\\ &\le& \pi \approx 0 \end{eqnarray}\] which holds for both marginal and conditional imbalance.
RFQ
The function imbalanced() of the package provides a RF implementation of the q*-classifier for the two-class imbalance problem. We refer to this method as random forests quantile classifier and abbreviate this as RFQ [2]. Currently, only two-class data is supported. We recommend setting ntree to a relatively large value when dealing with imbalanced data to ensure convergence of the performance value. Consider using 5 times the usual number of trees. The default value used by imbalanced() is ntree=3000.
The default performance metric used by imbalanced() is \[
\text{$G$-mean} =
\left(\textrm{TNR}\times \textrm{TPR}\right)^{1/2}.
\] The \(G\)-mean is the geometric mean of TNR and TPR and it is meant to replace misclassification rate in imbalanced data settings. The problem with the latter is that an overall accuracy close to 1 can be achieved by classifying all data points as majority class labels for heavily imbalanced data as previously noted. By way of contrast, the \(G\)-mean is close to 1 only when both the true negative and true positive rates are close to 1 and the difference between the two is small [3].
It is possible to use other metrics using the option perf.type, however we caution users to be careful when using these or other performance measures. We have already pointed out the problem with misclassification error, but there are other well known metrics that perform poorly in imbalanced data. An example is Area under the Curve (AUC) for Receiver Operating Characteristic (ROC), which we abbreviate as ROC-AUC. This is a widely used metric for classification, but ROC-AUC is insensitive to \(\mathrm{IR}\). Such a property is unwanted for imbalanced data since rare cases are usually associated with higher costs; proper performance metrics should show a monotonic decrease with increasing \(\mathrm{IR}\).
The following simulation illustrates this point. Classification data was simulated 100 times independently. Sample size and dimension was \(n=1000\) and \(p=25\). The data was made imbalanced with \(\mathrm{IR}\) values from 1 (balanced) to 100 (high imbalanced). A RF classifier was fit to the data and performance evaluated on an independent data set with sample size \(n'=20,000\). Test set performance was calculated for \(G\)-mean and ROC-AUC. Also included for comparison was AUC for precision recall, PR-AUC, which a metric suitable for imbalanced data [4]. To properly calibrate PR-AUC we normalize it by calculating the difference between PR-AUC for the RF classifier to PR-AUC for a completely randomized rule. The figure below displays the results. Both \(G\)-mean (figure a) and normalized PR-AUC (figure c) exhibit a monotonic pattern of decrease with increasing \(\mathrm{IR}\). This illustrates their suitability as performance metrics for imbalanced data. Note that PR-AUC does not measure performance of RFQ. This is because like all AUC methods it does not fix a threshold and instead hypothetically varies a threshold over all possible values in assessing performance. In contrast, \(G\)-mean directly measures peformance of RFQ. The results are very impressive. RFQ is able to perform very well even in high \(\mathrm{IR}\) settings of 100. Finally, notice that ROC-AUC (figure d) is insensitive to \(\mathrm{IR}\) which is a sign of optimistic bias. This metric is unsuitable for imbalanced data.
Variable importance (VIMP)
The standard variable importance (VIMP) measure in random forests introduced by Breiman and Cutler [5, 6], called Breiman-Cutler importance [7], permutes OOB data and runs it through the tree. The original OOB prediction error is then subtracted from the resulting OOB prediction error, resulting in tree importance. Averaging this value over the forest yields permutation importance. A positive VIMP signifies a variable that is predictive since permuting its value degrades tree prediction performance on average (VIMP vignette).
As detailed in [2], Breiman-Cutler importance is inappropriate for RFQ in the presence of significantly imbalanced data due to the fact that almost all nodes in an individual tree will contain zeroes. Instead, RFQ uses the \(G\)-mean to measure variable importance (VIMP). This is combined with Ishwaran-Kogalur VIMP, which is an ensemble rather than tree-based measure, defined as the prediction error for a blocked ensemble subtracted from the prediction error for the blocked ensemble obtained by permuting a variable’s data.
Illustration
library(randomForestSRC)
data(breast)
breast <- na.omit(breast)
o.rfq <- imbalanced(status ~ ., breast, importance = TRUE)
print(o.rfq)
> Sample size: 194
> Frequency of class labels: 148, 46
> Number of trees: 3000
> Forest terminal node size: 1
> Average no. of terminal nodes: 27.27967
> No. of variables tried at each split: 6
> Total no. of variables: 32
> Resampling used to grow trees: swor
> Resample size used to grow trees: 123
> Analysis: RFQ
> Family: class
> Splitting rule: gini *random*
> Number of random split points: 10
> Imbalanced ratio: 3.217391
> (OOB) Brier score: 0.18299786
> (OOB) Normalized Brier score: 0.73199144
> (OOB) AUC: 0.55581669
> (OOB) PR-AUC: 0.33327632
> (OOB) G-mean: 0.51419338
> (OOB) Error rate: 0.478714
>
> Confusion matrix:
>
> predicted
> observed N R class.error
> N 74 74 0.5000
> R 21 25 0.4565
>
> Overall (OOB) error rate: 47.871396%
plot(o.rfq, plots.one.page = FALSE)
get.imbalanced.performance(o.rfq)
> n.majority n.minority iratio threshold sens spec prec
> 148.0000000 46.0000000 3.2173913 0.2371134 0.5434783 0.5000000 0.2525253
> brier auc F1 balanced pr.auc.rand pr.auc gmean
> 0.7323268 0.5608108 0.3448276 0.5217391 0.2371134 0.3358875 0.5212860 
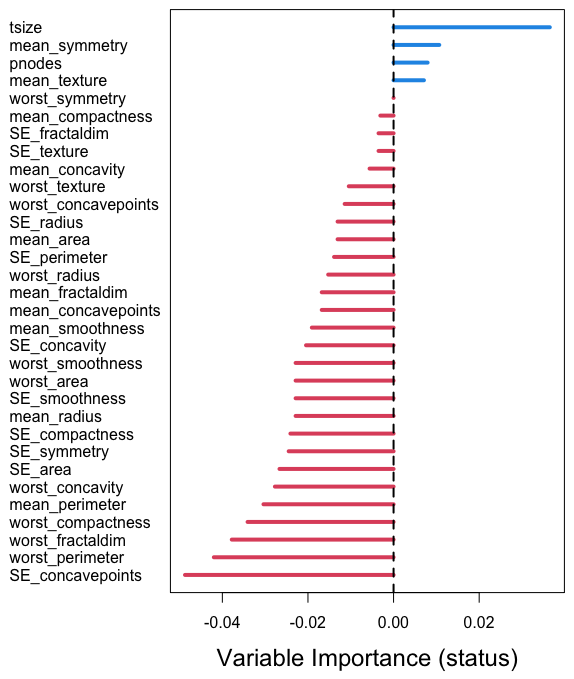
The above code is equivalent to setting rfq = TRUE, ntree = 3000, perf.type = "g.mean" in rfsrc when building the RF:
rfsrc(status ~ ., breast, rfq = TRUE, ntree = 3000, perf.type = "g.mean", importance = TRUE)To get the standard errors and confidence intervals for the VIMP, the function subsample() can be used (see VIMP vignette, [8]).
Cite this vignette as
H. Ishwaran, R. O’Brien, M. Lu, and U. B. Kogalur. 2021. “randomForestSRC: random forests quantile classifier (RFQ) vignette.” http://randomforestsrc.org/articles/imbalance.html.
@misc{HemantRFQv,
author = "Hemant Ishwaran and Robert O'Brien and Min Lu and Udaya B. Kogalur",
title = {{randomForestSRC}: random forests quantile classifier {(RFQ)} vignette},
year = {2021},
url = {http://randomforestsrc.org/articles/imbalance.html},
howpublished = "\url{http://randomforestsrc.org/articles/imbalance.html}",
note = "[accessed date]"
}